Ruled variety

In mathematics, a ruled variety is a variety birational to a product of the projective line and another variety, and a uniruled variety is a variety that is dominated by a ruled variety. This concept is a generalisation (not too remote) of the ruled surfaces of classical differential geometry.

A variety is uniruled if and only if there is a rational curve passing though every point.

Any uniruled variety has Kodaira dimension −∞. In dimension at most 3, and conjecturally in all dimensions, the converse is true: a variety of Kodaira dimension −∞ is uniruled.

Consequences of the Miyaoka-Mori theorem for smooth varieties

Let X be a smooth projective variety over an algebraically closed field and 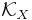$\mathcal K_X$ its canonical divisor. Then if there exists a curve C in X such that 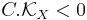$C . \mathcal K_X < 0$ , the variety X is ruled.

In particular, if X has nef anticanonical divisor, then for X to be ruled, it suffices for the anticanonical divisor to not be numerically trivial.

References

Clemens, Herbert; Kollár, János; Mori, Shigefumi (1988), "Higher-dimensional complex geometry", Astérisque (166): 144 pp. (1989), ISSN 0303-1179, MR 1004926